| In the Stochastic Analysis and Nonlinear Dynamics (SAND) lab our goal is to understand, predict, and/or optimize complex engineering and environmental systems where uncertainty or stochasticity is equally important with the dynamics. We specialize on the development of analytical, computational and data-driven methods for modeling high-dimensional nonlinear systems characterized by nonlinear energy transfers between dynamical components, broad energy spectra with complex statistics, and persistent or intermittent instabilities. We are particularly interested on the development of inexpensive predictive capacity for such systems as well as the development of design criteria for engineering applications. |
Recent News
- Paper on active learning for optimal interventions using causality models has been accepted to Nature Machine Intelligence and featured on the MIT News
- Paper on physics and forecasting of extreme separation events in airfoil flows has been accepted to AIAA Journal
- Stephen successfully defends his PhD thesis. Congratulations!
- Bianca receives multiple awards from MechE.
- Bianca and her work is featured at Spectrum. Congratulations!
Featured Papers
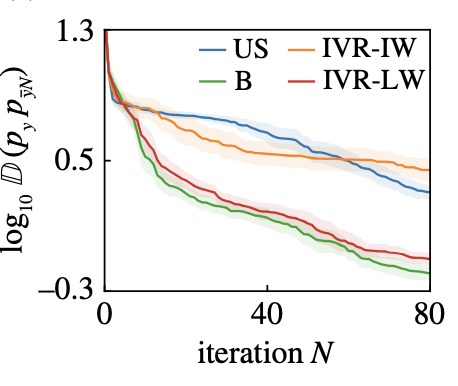 | Optimal acquisition functions for active learning of pdf tails T. Sapsis, A. Blanchard, Optimal criteria and their asymptotic form for data selection in data-driven reduced-order modeling with Gaussian process regression, Philosophical Transactions of the Royal Society A [pdf] |
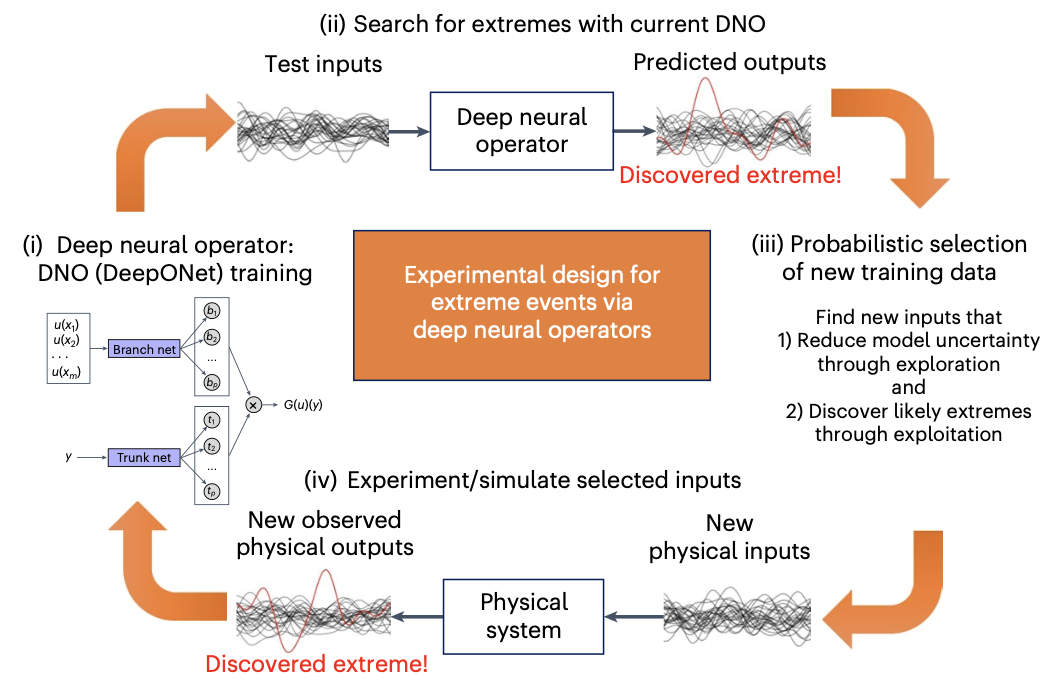 | Active learning with neural operators to quantify extreme events E. Pickering et al., Discovering and forecasting extreme events via active learning in neural operators, Nature Computational Science [pdf] |
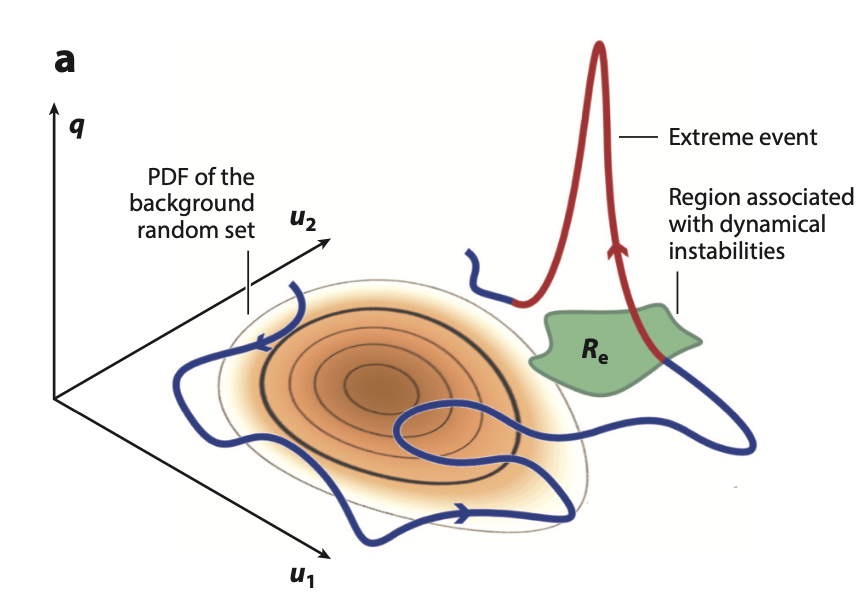 | A review of methods for modeling of extremes in fluids T. Sapsis, Statistics of extreme events in fluid flows and waves, Annual Review of Fluid Mechanics [pdf] |
 | Physically consistent NN closures for UQ of turbulent flows A. Charalampopoulos, T. Sapsis, Uncertainty quantification of turbulent systems via physically consistent and data-informed reduced-order models, Physics of Fluids [pdf] |